数学建模在军事问题上的应用

出自————《数学建模在军事问题上的应用》

出自————《现代军事理论》

　　 战争是一个非常复杂的问题，涉及因素很多，如兵员的数量和质量，武器的先进与落后，地理位置的有利与不利，指挥员的艺术、后勤供应、气候条件等。因此，如果把战争所涉及的因素都考虑进去，这样的模型是既难建立又难解决。但是对于一个通常情况下的局部战争，在合理的假设下选择主要因素建立一个作战数学模型，我们将会看到得出的结论是具有普遍意义的。

　　 在第一次世界大战期间，F·W·Lanchester就投身于作战模型的研究，并得到了一些可以从中得到交战结果的数学模型。

　　 对于一次局部战斗，有些因素可以不考虑，如气候、后勤供应、士气等，而有些因素可认为是双方是相同的，如武器配备、指挥艺术等。

　　 模型1 正规战争模型

　　 令x(t)表示t时刻甲军人数，y(t)表示t时刻乙军人数，假设

　　 (1) 每一方人数减员率与另一方人数成正比；

　　 (2) 两军士兵都处于双方火力范围内；

　　 (3) 不考虑双方支援部队；

　　 (4) 双方的初始兵力分别是和。

　　 由以上假设可得正规部队的作战模型为

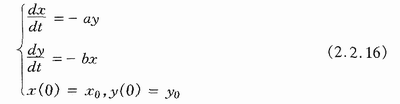
　　 其中a>0，b>0均为常数，表示战斗系数。

　　 积分（2.2.16），得

　　 这就是著名的“Lanchester平方定律”。（2.2.17）式在 x-y 平面上是一簇双曲线，如图2.2.4所示。双曲线上箭头表示战斗力随着时间而变化的方向。

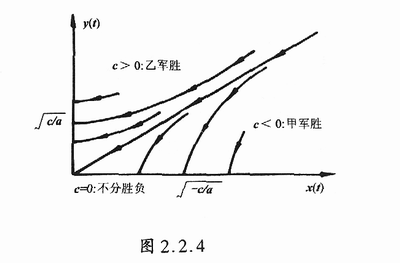
　　 可以看出，如果 c > 0，轨线将与y轴相交，这就是说存在，使，，即当甲方兵力为零时乙方兵力为正值，表明乙军获胜。同理可知c<0时甲军获胜。当c=0时双方战平。

　　 进一步分析可知，乙军要想获胜，既要使>成立。可采用两种方式：（1）增加 a，即配备更先进的武器。（2）增加最初投入战斗的人数。但是值得注意的是：在（2.2.17）中，a 增大两倍，结果也增大两倍，但增大两倍则会使增大四倍。这正是两军摆开战场作正规战时Lanchester平方定律的意义，说明兵员增加战斗力将大大增加。

　　 为此我们考虑有增援情况的战争模型。即除了模型1的基本假定之外，进一步假设f(t) 和g(t)分别表示甲军和乙军t时刻的增援率。（所谓增援率，就是增援战士投入战斗或战士撤离战斗的速度）。此时正规作战模型为：

　　 模型2 混合战争模型

　　 如果甲军是游击队，乙军是正规部队，由于游击队对当地地形熟，常常位于不易发现的有利地形。设游击队占据区域R，由于乙军看不清楚甲军，只好向区域R射击，但不知道杀伤情况。为此，我们假设：

　　 游击队x(t)的战斗减员率应当与x(t)成正比，（因为x(t)越大，目标越大；被敌方子弹命中的可能性越大）。

　　 游击队x(t)的战斗减员率还与y(t)成正比，（因为y(t)越大，火力越强，x(t)的伤亡人数也就越大）。

　　 游击队和正规部队的增援率分别为f(t)和g(t)。

　　 由以上假设可知，游击队的战斗减员率等于cx(t)y(t)，作战模型为

　　 其中c称为敌方y的战斗有效系数。

　　 若无增援f(t)和g(t)，则

　　 积分（2.2.20）式得

　　 （2.2.21）式在x-y平面上定义了一簇抛物线，如图2.2.5。

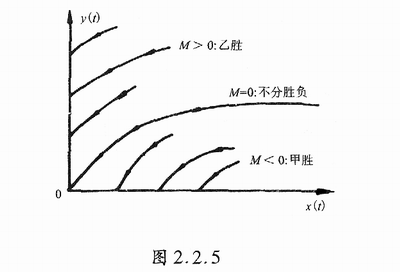
　　 如果M>0，则正规部队胜。因为当y(t)减小到，游击队x(t)已被消灭。同样，如果M<0，则游击队胜。

　　 几点说明

　　 (1) 在模型（2.2.18）中，如果a，b，f(t)和g(t)已知，则可用显示求解。在模型（2.2.19）中，因方程组是非线性的，求解困难，可利用计算机求解。

　　 (2) 事前确定战斗系数a、b、c和d的数值通常是不可能的。但是如果对已有的战役资料确定a和b（或者c和d）的适当系数值，那么对于其它类似于同样条件下进行的战斗，a和b（或c和d）这些系数可认为是已知的。

　　 (3) 由（2.2.20）式有

　　 利用上式可以估计出正规部队要取得胜利需投入多少初始兵力。美国人曾用这个模型分析越南战争，以及二战时美国和日本硫黄岛战役，发现模型结果与实际数据吻合的很好，这就说明Lanchester作战模型是能够用来描述战争的。有兴趣的读者可参考有关文献。

　　 (4) 上述模型没有考虑交战双方的政治、经济、社会以及自然环境等因素，因而仅靠战场上兵力的优劣是很难估计战争胜负的，所以我们认为用这些模型判断整个战争的结局是不可能的，但是对于局部战役来说或许还有参考价值。更重要的是，建模的思路和方法为我们借助数学模型讨论社会科学问题提供了可借鉴的示例。